Lab 1 - Beginning Problem Solving¶
Note
This exercise will not use Python, just your brain. You will need to write up your solution using a text editor. You can use any editor you like, or use Notepad. Even better, use gVim. You will submit this by adding it to your “working copy”, then uploading it to the GitHub. Those notes come next
What does this mean?¶
x = sqrt(5)
If you own a calculator, you can probably figure this out. The sqrt thing
is called a function. A function is a magical gadget that can do some
work for you. We do not need to know how this magic happens most of the time,
that is what the calculator is for. But what if you needed to design the
calculator. How will you get the magic to happen?
You should have run into these function things in your math classes. How you
get out the actual value for x without using a calculator was probably left
as a puzzle for you to figure out. Let’s try to do that here!
Warning
Many students assume I want just the square root of “5”. Actually, the user will tell you what number they want to use, and it will probably not be five!
Back to your math class¶
You probably saw something like this in your math text:
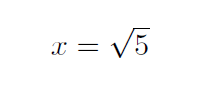
This is an equation. The two things on either side of the = symbol are
supposed to be equal. (That is why we call it an equal symbol - DUH!)
You were probably also told that if you figured out the right value for the
x thingy, this equation would be true as well:
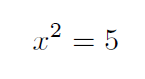
Now, most computers cannot generate that funny little 2 in that equation,
so we will show it this way instead:
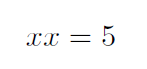
Now we have another problem. Many math books show things this way, but how do
we really know that xx means x times x? (I know, you saw it written
this way a lot, and the symbols were always one character long.) We will solve
this problem by using a new symbol for multiplication (no, we will not use
x that would really get confusing. Instead, we will use a star: *. So
that last equation would look like this:
x * x = 5
That * symbol means multiply. Got it all figured out now?
The question we want to address in this lab is simple.
How do we go about figuring out the right value for ``x``.
Your problem¶
Suppose you have a pocket calculator that can only do multiplication. How would you approach figuring out the answer? Think about this, and try to come up with a scheme that will give you the answer. Do not just use simple trial and error, think about how you might get an accurate answer. You might start off with a one digit guess, like 2 or 3, then add a digit after the decimal point to refine your guess. Your calculator will help you check your guesses.
No fair just turning to google to find the scheme. You need to start thinking
problems through by yourself. So do your own thinking about this, remembering
that we are trying to teach a computer how to do the work. The goal is to
produce a list of the steps needed to figure out the right value for x
using just the multiply key on the calculator
Note
If you do not happen to own a calculator, there is one on your computer. Go
to Start -> All Programs --> Accessories --> Calculator. (There will
be a square-root key on that calculator. You may use it only to see what
the right answer is, not to figure out the answer.
Checking your work¶
You should write down the process you come up with clearly enough that another
person could use your process to figure out the answer. See if you can get
someone else to try it out with a calculator. You should also try it yourself.
In this case, pretend you never saw this process before and follow it
exactly. If you get the answer, you done good!
What to turn in¶
Once you think you have a solution, write it up using the example pseudo-code shown in the notes. Nothing fancy is required, do the best you can. We are learning new stuff here, so try to be clear.
Save your work in a file named “SquareRoot.txt”. If you named it something else, you can rename it before turning it in.
Refer to the next lecture which introduces Git, to see how to turn this all in. Don’t panic if you have a hard time coming up with an answer to this, it takes time (and practice) to get used to this thinking stuff!
