Formally Defining Languages

Read time: 41 minutes (10264 words)

We create special languages for use in programming a computer. These languages are very different from the ones we use as humans, to communicate with other humans. Programming languages must not allow any ambiguity. Each “sentence” in the programming language must be clear enough to allow conversion of that sentence into a form the computer can process. Furthermore, the computer’s operation, when processing that sentence, must match the programmer’s understanding of what that sentence “means”.

We call the precise form of a sentence the syntax of that sentence, and we call the meaning of that sentence the semantics of that sentence.

Designing programming languages in a formal way has been studied for quite a while, and you will earn all about this in a compiler course later in your education. Since we will be learning new languages in this course, it is worth taking a quick look at one of the most common ways computer languages are defined.

EBNF

Niklaus Wirth, who has designed a number of popular programming languages, including Pascal, proposed a formal notation to be used in specifying programming languages in a paper he authored in 1977 [[Wir77]]. The notation is called Extended Backus-Naur Form or EBNF. As you might expect from the name, it is an extension of another, sightly more complex notation that was being used up to that time.

Basically, EBNF lets you define a set of rules that define the grammar for a language. ENBF says nothing about what to do with that grammar, but the rules can help you build tools that will process programs written in the language defined.

The EBNF notation, itself, can be described using this notation. We will do that here. In the description of EBNF below, we will use something called a railroad diagram to show a rule. Later, we will ditch the diagrams and use something you can write in your favorite editor.

Grammars

We call the formal set of rules we create to define any language a grammar. The rules are just like those you learned back in elementary school. Back then, you learned the rules for forming sentences in the language you were learning. In programming, we call sentences statements. Same idea. If the sentence is malformed, it will not make any sense. If the program statement does not follow the rules, the compiler will not be able to figure out what you want it to do.

Here is the rule that defines a grammar:

grammar::=

The reason this diagram is called a railroad diagram should be obvious. Those lines look like train tracks, with switches allowing you to travel one way or another. When we use these rules to create programs written in the language being defined, we will start at the left side of this top-level rule, with no code in the file. We will then travel to the left along the tracks and do one of two things.

If we encounter a block (such as the production block above), we will stop traveling along this rule, and jump to the rule with the name inside that block (‘’production`` here). This is much like a function call, and we will be coming back to this rule once we have completed travel over that production rule. We will then continue along this first grammar rule, following the tracks, until we reach the end of the rule on the right side. Since this is the first rule, the one we started working with, when we reach that right side, we stop. We have completely define the thing called a grammar!

The second thing we do while traveling along a track is figure out what to do when we reach a switch. At those points you can either continue along in a straight line, or take the switch until you run into another block (or switch). In the diagram above, it looks like a grammar can be formed out of one or more production things. That is exactly right. You must have at least one production in your grammar, but you might have more than one.

The decision on which path to take at a switch is usually easy, at least in well designed languages. Each possible path will eventually lead to another rule that beginning with something easy to identify. For example, in most programming languages, statements always begin with a reserved word, chosen to help identify that statement. Words like if, while, and for should all be familiar to you by now. As soon as you see that word, you know what should come next, and what rule you want to be processing in the grammar.

Obviously we need a bunch more rules, since we have not entered anything into our code file yet.

Productions

Here is the production rule:

production ::=

Note

There is one special thing on thing in this rule. There is a semicolon in a block at the end of this rule. That means that every production must end with a semicolon. (More on that curved-corner box in a bit.)

We are making progress, except this rule immediately runs into another rule block, but this one is named identifier, We sort of have an idea what that might be. As programmers, we create identifiers all the time, only we call them variable names or function names. Since this is another rule, we might suspect that there is a rule telling us what makes up a legal identifier in this language. (Sound familiar?)

We still have not entered a single letter into our code file. Let’s follow this rule and see where we go:

Identifiers

Finally, a rule we can use to enter some text into our program file:

An identifier is defined by this rule:

identifier ::=

Shoot, yet another rule for something called a letter. The reason we use this rule is simple. Not every language you run into will let you use just anything you like for names. We might restrict the names to all capital letters (that seems silly, but that used to be the rule in some languages).

Here is the end of this chase:

Letters

Now, we end up with rule that let us type something:

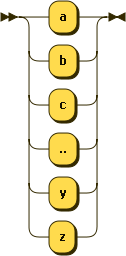
letter ::=

Note

This rule is just silly. You mean we have to list every letter we will allow. Yes, you might want to do that to have complete control over what the language allows. I actually cheated in this diagram. EBNF does not allow that “..” thing. I used it to keep this diagram short! The meaning should be clear.

The bold text in this rounded-corner box tells you this box is different from that production box we started with. The round corner box is not another rule. Instead, you will be typing in exactly what you see as you see in this block. That means we are only allowed to use lower-case letters in this language. We could extend that, but we will leave it as it stands for now,

Productions Revisited

We did not fully complete the description of that production rule.

A production will be defined with a name (the identifier). We will use that name in other rules (they will show up as blocks with that name inside). The actual rule that defines how to write this production is given following the “::=” text string, you are required to write in your rule.

Note

Remember, we are showing these rules as pretty diagrams here, the actual grammar is written in a simple text file we will see later.

The hard part of defining what a production looks like is the next block, an expression.

Expressions

You have used expressions in your programming. They are complicated strings of text made up of variable names, numbers, math operators and parentheses. Our expressions will be a bit like that, but the notation is different.

Here is our top-level rule for an expression:

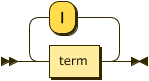
expression ::=

This does not look so bad. An expression is just one or more term things separated by a vertical bar character (“|”). This diagram is actually defining a set of alternatives you can select from. The rule will add those switches to the diagrams you might generate for your language .

Note

The diagrams you are viewing in this note were generated on a website that takes an EBNF notation and produces the image you see. Here is the website I used: Railroad Diagram Generator. The actual rule set I used in creating this note are included at the end of this lecture

Terms

Believe it or not, we are making progress. Only a couple more rules and we will be done.

A term looks like this:

term ::=

Still pretty simple.

Finally we get tho the real fun diagram:

Factor

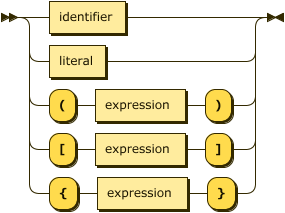
factor ::=

This one is a bit complicated, because it has several paths we can follow.

The simple path is just an identifier, which is the name of some other rule. Then we have a literal, which is just something in quotes (either single or double will do). Those quoted strings mean that you must type in exactly what you see between the quotes (not the quotes themselves). In the diagrams those strings show up in bold.

The paths that go through square brackets are the optional things. They can either be included in your program, or not.

The path through the curly brackets are repeated things. They can appear zero (meaning they are missing) or as many times as you like.

Phew.

The EBNF Rules in EBNF

Here are all of these rules shown in text form. See if you can see how the diagrams match up with these rules.

grammar ::= { production } ;

production ::= identifier "::=" expression ";" ;

expression ::= term { "|" term } ;

term ::= factor { factor } ;

factor ::= ( 
      identifier 
    | literal 
    | "(" expression ")" 
    | "[" expression "]" 
    | "{" expression "}" )
    ;

literal ::= ( 
      '"' character { character } '"' 
    | "'" character { character } "'" ) 
    ;

identifier ::= letter { letter | digit } ;

Notice that I used parentheses to surround some of these complex rules to make sure they followed the rules properly. You run into this kind of thing all the time when defining languages, and this one was pretty simple!

This rule set is not really complete, but it is close enough for now. We left undefined the letter and character blocks. Basically a letter will be a lower-case alphabetic character, and a character will be any printable thing you can type on your keyboard. It would be messy to completely define that in a rule (but we could).

Diagram Tool Rules

The website I used to generate the diagrams seen in this note uses a slightly different scheme for writing the rules. We will not go into detail about the differences, but you should be able to figure these rules out by looking at the website itself. They have documented how to set things up to get the diagrams.

grammar ::= production+
production ::= identifier "::=" expression ";"
identifier ::= letter+
expression ::= term ( "|" term )*
term ::= factor+
factor ::= identifier | literal | "(" expression ")" | "[" expression "]" | "{" expression "}"
literal ::= '"' character+ '"' | "'" character+ "'"

I do not expect you to be able to define a language on an exam in this course, but you should be able to follow an EBNF rule and understand what it tells you to do when you write something in the language we are studying.

Apple Pascal Poster

Reference

http://www.pascal-central.com/pascal-syntax.html

Back in the early 1980’s I taught beginning programming classes using Wirth’s Pascal Language. Pascal was so popular that Apple published a single sheet poster defining the entire language. No self-respecting programmer in those days would be caught programming without this poster hanging on the wall behind their terminal (The PC had not been invented yet!):

With this background in language design, let’s take a look at a simple C++ program.