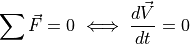Ball Physics¶
Read time: 39 minutes (9905 words)
We will be working on a pool ball simulation in class, so we need to understand a few things about how a pool ball moves. We also need to understand what happens when we put a lot of moving balls on a table. You already have an idea what happens, but we need to figure out the math needed to calculate exactly what happens.
Stand by, this is interesting. (Even if you hate math!)
Newton’s Laws¶
We start off by looking at three laws from Physics, created by Isaac Newton back in 1687 [newton:1687]
Inertia: Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it.
The change of momentum of a body is proportional to the impulse impressed on the body, and happens along the straight line on which that impulse is impressed.
- To every action there is always opposed an equal reaction: or the mutual
actions of two bodies upon each other are always equal, and directed to contrary parts.
The wording back then was a little, well, dated! (Or, is it us?)
Basically, these three laws tell us how a pool ball will move along on a table with walls all around (we will ignore pockets).
Moving a Ball¶
We will place a ball on the screen at some point, and begin a simulation loop that models the passing of time. Each pass through the loop represents one unit of time. During that time, the ball will move to a new position. If we draw the ball at the starting point, then erase it and redraw it at a new point after that period of time, it will look like the ball moved.
All we need to do is track the current position of the ball, and the velocities
of that ball in the X direction (left to right) and in the Y direction
(down to up). The “speed” of the ball is the vector sum of these two
velocities.
Phew, physics!
If we make the speed of the ball in each direction the number of pixels the
ball moves each pass through our loop, all we need to do to calculate a new
position is add the speed in the X direction to the X``position of the
ball, and do the same for the ``Y position:
Xball = Xball + DX;
Yball = Yball + DY;
Here, I am using DX to indicate the speed of the ball in the positive X
direction (to the right), and DY to represent the speed of the ball in the
positive Y` direction (up).
Obviously, big numbers for DX and DY will make the ball appear to move
faster!
Once we set a ball in motion somehow, it will continue moving in that direction until something interferes with that motion. If all we are dealing with is a single ball moving on the table, we will eventually run into a wall. Exactly what happens then is our first challenge.
You know what will happen, but how to we model that action in a simple simulation?
Bouncing¶
Suppose the ball is moving straight toward the right wall and bumps into it.
What will happen? The wall will not move, and according to Newton’s laws, all
of the energy that ball has will cause it to move away from the wall at the
exact speed it had when approaching the wall. That means if the speed of the
ball toward the wall was DX, when we move away, after bouncing, the new
speed will be -DX. All we need to do when we detect that the ball has hit
the all is flip the sign on whatever value is currently stored in DX and
the ball will move away from the wall.
Bounce!
The same thing happens on all other walls as well.
Angular Bouncing¶
What if the ball is approaching a wall at an angle? Well, that means DY in
our first example is not zero. But the “bounce” calculations still apply. THe
movement in the X direction needs to be modified, but not in the Y
direction. The ball will continue to move in the Y direction with the same
speed as before!
Think about what happens if you throw a ball toward the floor away from you. It bounces away from the floor when it hits that floor, but continues to move away from use as before.
So, we “bounce” off of any wall, by doing these modifications:
Bounce off of left or right walls:
DX = -DXBounce off of top or bottom walls:
DY = -DY
Detecting the Wall¶
The last thing we need to figure out is how to determine if the ball has hit the wall.
You will know where the walls are! You set up the graphics window with a
specific width and height (both of which are defined in the Graphics.h file
in your graphics library. You are tracking the current position of the ball
with attributes stored in the ball object. All you need to do is compare those
two values to see if you have made contact.
Right? Wrong!
It is not the center of the ball that bounces off of a wall, it is the edge of the ball. So your check needs to account for the radius of the ball, which we also have recorded in the ball attributes.
Coding the Action¶
Putting all of this together is pretty basic stuff. You need a few computations to verify where the ball is in relation to each of the four walls, then you adjust the appropriate speed variable according to the rules above, and watch as the simulation loop spins! The ball should “bounce” off of all four walls.
Reality Check!¶
Does a real pool ball just bounce forever? No! It slows down as it moves, eventually stopping. We can model that by adjusting the total speed of the ball by some small amount on each pass through the simulation loop.
The total velocity is the “vector sum” of the velocity in the X and Y
directions. We could figure out that number, then multiply that velocity by
some small number, like 0.999, then figure out the two speed components from
that new number. We could do that, but that is silly. Just multiply both
DX and DY by that one number, and you have a new velocity. What we just
did was account for “friction” between the table and the ball. That is Newton’s
force modifying the speed. Fun!
Note
In a course I taught at Texas State, I also added a slight “gravity”
feature to the movement, which simulated a table that was not level. In
that case, gravity will tend to “pull” the ball toward the low side of the
table. I simply added a tiny amount to the speed in the Y direction
(actually, a tiny negative number) to make the speed increase in a downward
direction, and it looked pretty cool!
One Last Point¶
We will not be able to make the ball hit a wall exactly. That DX number we
are adding to the X position of the ball will make the edge of the ball
miss the exact edge of the wall. The best we can do is detect that the ball has
moved too far, and not sides slightly inside oe the wall. If our movements are
small, and the loop runs fast, we can ignore this slight imperfection and just
detect when we are clearly supposed to bounce. We flip the sign on the
appropriate speed variable, and the ball will begin to move away. The viewer of
our action will not notice this error.
When Balls Collide¶
The math required to figure out what happens when two balls collide is pretty hairy, but not exceedingly difficult to figure out. Basically, we need a bit more “vector algebra” to come up with the new velocities. We will not go over that math here, it is easy enough to find on the INternet, or think through yourself. Basically all we need to do is calculate the distance between any one ball and all others on the table and see if there has been a collision. That will happen when the distance between those two balls is smaller or equal to the sum of the two radii. Once we know that, we know where the two balls are, how fast they each are moving in each direction, and we have anew “bounce” to firure out.
That is where the math gets ugly. You need to “project” the total velocity of both balls onto a new coordinate system that is aligned with a line between the two ball centers. The other coordinate line will run perpendicular to that first line, right at the point of contact. The “bounce” will happen the same as before. The velocities toward that contact point will be adjusted, and the velocities in the other direction will remain the same. I will leave this discussion at that, and simply show the formulas we can use:
..`code-block:: c++
// see if ball i collided with ball j double dist, x1, x2, y1, y2, dx, dy; double vx1, vx2, vy1, vy2; x1 = xPos[i]; x2 = xPos[j]; dx = x2 - x1; y1 = yPos[i]; y2 = yPos[j]; dy = y2 - y1; dist = sqrt((dx*dx) + (dy*dy)); if (dist > 2.0 * RADIUS) return; // no collision
double ax, ay, vn1,vn2,vt1, vt2, v1np,v2np, v1tp, v2tp;
ax = dx/dist; ay = dy/dist; vx1 = deltaX[i]; vx2 = deltaX[j]; // X velocities vy1 = deltaY[i]; vy2 = deltaY[j]; // Y velocities
vn1 = (vx1 * ax + vy1 * ay); vt1 = (-vx1 * ay + vy1 * ax); vn2 = (vx2 * ax + vy2 * ay); vt2 = (-vx2 * ay + vy2 * ax);
v1np = vn1 + (vn2 - vn1); v2np = vn2 + (vn1 - vn2);
vx1 = v1np * ax - vt1 * ay; vy1 = v2np * ay + vt1 * ax; vx2 = v2np * ax - vt2 * ay; vy2 = v2np * ay + vt2 * ax;
deltaX[i] = vx1; deltaY[i]= vy1; deltaX[j] = vx2; deltaY[j]= vy2;
Warning
This code is not quite correct, and if you run a program using this, your actions will be a bit off at times. Figuring out why, I will leave as an exercise.
There is one serious flaw with the above code, beyond that warning above. Sometimes two balls will seem to stick together, which is definitely not real! Why this happens has to do with that point above where we discussed moving “into” a wall. In this case, the two balls move into each other, and when they bounce away, they might not fully move apart. On the next pass through the loop, they will seem to bounce again, and get stuck further. They stay that way until something (like another ball striking one of them) causes them to finally move apart. I have left this code this way for years, because it is fun to watch the funny actions.
One final note. In the logic that detects if two balls collide, you need to
remember that if ball i and ball j have collided, you do not want to
consider if ball j has collided with ball i. If you do that, you will
“un-bounce” something you already handled. The fix is in the collision detection
loop: every ball must be checked against every other ball, unless that
collision has already been handled!
Here is the logic needed:
for(int i = 0; i < NUMBALLS -1; i++)
for(int j = i + 1; j < NUMBALLS; j++ )
check_collision(i,j);
You now have enough code to handle a single ball bouncing around on the table, or (if you are brave enough, a slew of bslls swarming around. Have fun with this!