Bouncing off Walls¶

Read time: 29 minutes (7429 words)

Once we start moving the poolball on the screen we need to watch out for collisions!

To view our simulation, we need to add graphics to our code. the basic graphics library provided in your setup lab is not quite up to the job we need. I added a few parameters to that code so you can size and position the window when you start the program. Here are the new files you need:

Graphics.h

Graphics.cpp

Replace the current files with these for your Poolball work.

Poolball Implementation¶

The Poolball is a pretty basic piece of code. In modeling the behavior of the ball, all we need to do is figure out how to make the ball move. However, once we decide to add graphics to the program, we need to draw the balls on the screen.

We can do this one of two ways. Either we let the ball draw itself, which it can do since it knows its own position, or we let the management class (Pooltable) do that job.

If we move the drawing responsibility to the Pooltable, we will need to provide access to the ball attributes to figure out what to draw. Programming always involves design decisions that affect the code you write.

For now, we will let a ball draw itself!

Here is the basic code we need:

lib/Poolball.cpp¶

// Copyright 2019 Roie R. Black
#include "Poolball.h"


// constructors
Poolball::Poolball(void) {
    xPos = 50;
    yPos = 50;
    radius = 25;
    xSpeed = 2;
    ySpeed = 2;
    radius = 25;
    color = BLUE;
}

Poolball::Poolball(float x, float y, float r, float vx, float vy, ColorName c) {
    xPos = x;
    yPos = y;
    radius = r;
    color = c;
    xSpeed = vx;
    ySpeed = vy;
}

// mutator methods
void Poolball::setXpos(float pos) {
    xPos = pos;
}

void Poolball::setYpos(float pos) {
    yPos = pos;
}

void Poolball::setXspeed(float speed) {
    xSpeed = speed;
}

void Poolball::setYspeed(float speed) {
    ySpeed = speed;
}

void Poolball::move(void) {
    xPos += xSpeed;
    yPos += ySpeed;
}

// accessor methods
float Poolball::getXpos(void) {
    return xPos;
}

float Poolball::getYpos(void) {
    return yPos;
}

float Poolball::getRadius(void) {
    return radius;
}

ColorName Poolball::getColor(void) {
    return color;
}

float Poolball::getXspeed(void) {
    return xSpeed;
}

float Poolball::getYspeed(void) {
    return ySpeed;
}

void Poolball::draw(void) {
    setColor(color);
    drawFilledCircle(xPos, yPos, radius);
}

This code is fine for handling one Poolball. However, when we have more than one ball moving on the table, we have a problem.

Who Watches For Collisions?¶

We need a management class, responsible for making sure all Poolballs move properly on the table. We also need this class to watch what is happening, and cause “collisions” to be taken care of! We have not put any collision detection logic in the Poolball class, since the ball cannot “see” what is around it!

The Pooltable class is pretty simple:

include/Pooltable.h¶

// Copyright 2019 Roie R. Black
#pragma once

#include "Poolball.h"
const int MAXBALLS = 5;

class Pooltable {
 private:
    int width;
    int height;
    int ball_radius;
    Poolball balls[MAXBALLS];
    void checkWallCollisions(void);

 public:
    // constructor
    Pooltable(int w, int h);

    // mutators
    void placeBalls(void);
    void move(void);

    // graphics
    void draw(void);
};

Here is the implementation of the POoltable class:

lib/Pooltable.cpp¶

#include "Pooltable.h"

// constructor
Pooltable::Pooltable(int w, int h) {
    width = w;
    height = h;
    ball_radius = 25;
    placeBalls();
}

// mutators
void Pooltable::checkWallCollisions(void) {
    // loop over all balls
    for (int i = 0; i< MAXBALLS; i++) {
        // check bottom wall
        if(balls[i].getYpos() < ball_radius) {
            balls[i].setYspeed(- balls[i].getYspeed());
        }
        // check top wall
        if(balls[i].getYpos() > height - ball_radius) {
            balls[i].setYspeed(- balls[i].getYspeed());
        }
        // check left wall
        if(balls[i].getXpos() < ball_radius) {
            balls[i].setXspeed(- balls[i].getXspeed());
        }
        // check bottom wall
        if(balls[i].getXpos() > width - ball_radius) {
            balls[i].setXspeed(- balls[i].getXspeed());
        }
    }
}

void Pooltable::move(void) {
    for(int i=0; i<MAXBALLS; i++) {
        balls[i].move();
        checkWallCollisions();
    }
}

void Pooltable::draw(void) {
    for(int i=0;i<MAXBALLS;i++) {
        balls[i].draw();
    }
}

void Pooltable::placeBalls(void) {
    for(int i = 0; i < MAXBALLS; i++) {
        balls[i].setXpos(50 * (i+2));
        balls[i].setYpos(50 * (i + 3));
        balls[i].setXspeed(i + 1);
        balls[i].setYspeed(i + 3);
    }
}

The constructor is pretty simple, since all we need to do for now is record the table dimensions. We will need those as we track the positions of the balls to see if they hit the edges of the table.

The table moves all the balls by simply looping over each one, calling the ball move method. Then the table needs to check to see if any of the balls hit a table edge. THat is handled in the checkWallCollisions method.

Drawing all the balls is another simple loop, however we need to think about this:

Let’s consider two ways we might shape a graphics program that draws poolballs on a screen:

while (!keypressed()) {
    myscreen.erase(ball);
    ball.move();
    myscreen.display(table);
    myscreen.display(ball);
}

Why did I write it this way? Why not just call one simple routine to do all this work in one step? Like this:

while (!keypressed()) {
   myscreen.updateScreen(ball);
}
...
MyScreen::updateScreen(Poolball ball) {
    ...
    ball.move();
    ...
}

What will happen here? Well, we call the updateScreen method and send down a copy of the ball object. Inside the routine we call the ball’s move method which will update the instance variables to make the ball move. But, what variables were updated? Unfortunately, not the original ball’s, but the copies! That is not good. When we exit the updateScreen function, all those changes inside the object are lost, just like they would have been in a simple value parameter.

We can solve this problem by passing a reference to the object, in which case modifications to the object inside the function will be made to the original object. It is far too easy to forget all of this when you first start writing object oriented code using your normal way of thinking.

We have not really answered the question! Is a bit-wise copy of the object adequate. In this problem, the answer is yes, but in many cases, the answer is emphatically NO! We can see a glimmer of why in our Poolball object. Contained inside that object are a number of attributes, each with unique values. If we copy whatever is currently in those attributes, will everything still work?

In this simple case, everything might work, as long as those copies do not get modified, just used. For example, we can pass a copy of the ball to a drawing routine, confident that the copy will remain unchanged. But as our objects get more complicated, the answer might not be so clear. As we build more complex objects, we will need to revisit this whole copying issue.

Moving a bunch of balls¶

We have provided most of the code needed to build our complete Poolball demo. We have not explained how to make balls bounce off of each other, though.

Well, first, we came up with a way to determine if the ball had even hit the wall. We did this by calculating how far the center of the ball was from the wall. If that distance was less than the radius of the ball, we trigger a bounce. Since our simulation is working by moving a clock forward in distinct ticks, we will not be able to see the exact moment a collision happens, but we will be close enough for our demonstration purposes.

Now, how will we determine if one ball has hit another ball - given that we have a number of them?

We have created an array of Poolball objects as a simple way to manage the collection. The Pooltable object is responsible for watching each and every Poolball object, and that includes watching to see if they have hit a wall, or another ball. The two events are different, and involve different calculations.

Bouncing off the walls¶

Here is the logic we need to add to our Pooltable class to make it watch the wall collisions for every ball in our array of balls:

// now loop over all the balls in the simulation
for(int i=0;i<MAXBALLS;i++) {

    // let this ball move
    balls[i].move();

    // see if we hit the wall
    if (balls[i].getX() >= (width - rad))
        balls[i].setVx(-balls[i].getVx());
    else if (balls[i].getX() =< rad)
        balls[i].setVx(-balls[i].getVx());
    if (balls[i].getY() >= (height - rad))
        balls[i].setVy(-balls[i].getVy());
    else if(balls[i].getY() <= rad)
        balls[i].setVy(-balls[i].getVy());
}

See how this works? We loop over all balls in our collection moving each and then checking to see if any of the four walls have been hit. If so, we adjust the velocity according to rules we discussed earlier. Why do I check the walls this way? It is possible that we hit two walls at the same time, so we allow that to happen. (It is not possible to hit both vertical or horizontal walls at the same time, though).

Bouncing off each other¶

The logic for managing the ball-to-ball collisions is similar. Except now we need to check every ball against every other ball and see if we need to adjust the velocity. Here is a loop that might do the job:

for(int i=0;i<MAXBALLS;i++) {
    for(int j=0;j<MAXBALLS;j++) {

        // skip a ball hitting itself
        if (i == j) continue;
        checkBallCollision(i,j);
    }
}

We skip the obvious situation where a ball collides with itself, and check every other possible collision. If you think about it, we could end up checking every actual collision twice - once for each ball involved in the collision. A simple (and totally wrong) method for simulating the collision is to treat the second ball in the collision as a fixed wall that is aligned perpendicular to the line between the centers of the two balls and just bounce the same way we did with the table walls.

Why is this wrong? Well, when two balls moving at different speeds run into each other, we need to determine how the shared momentum of those balls is redistributed back into each ball, and set each ball’s new velocity correctly. This involves more work than I want to go through here, so I will do the simple (and wrong) thing and see what it looks like!

Here is the situation:

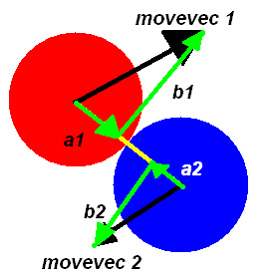
What we need to do is to break the total velocity of each ball into two parts, one along the line between the two centers, and one perpendicular to that line. We will bounce the ball by reversing the normal part, then recalculating the velocity in the x and y directions so we can update the ball’s velocity. Simple, huh? Yep, except for the math. Which is here:

dx = x2 - x1;
dy = y2 - y1;
dist = sqrt(dx*dx+dy*dy);
if (dist < 2.0*radius) {
    // they did, adjust their velocity
    double phi; // angle between the two ball centers
    // watch for vertical hits
    if(dx == 0.0)
        phi = PI/2.0;
    else
        phi = atan2 (dy, dx);

    // now compute the total velocities of the two balls
    double vx1 = balls[i].xVelocity;
    double vy1 = balls[i].yVelocity;
    double v1total = sqrt(vx1*vx1 + vy1*vy1);
    double vx2 = balls[j].xVelocity;
    double vy2 = balls[j].yVelocity;
    double v2total = sqrt(vx2*vx2 + vy2*vy2);

    // find the angle of each ball's velocity
    double ang1 = find_angle(vx1,vy1);
    double ang2 = find_angle(vx2,vy2);

    // transform velocities into normal.tangential components
    double v1xr = v1total * cos(ang1 - phi);
    double v1yr = v1total * sin(ang1 - phi);
    double v2xr = v2total * cos(ang2 - phi);
    double v2yr = v2total * sin(ang2 - phi);

    // now find the final velocities (assuming equal mass)
    double v1fxr = v2xr;
    double v2fxr = v1xr;
    double v1fyr = v1yr;
    double v2fyr = v2yr;

    // reset the velocities
    balls[i].xVelocity = cos(phi)*v1fxr + cos(phi+PI/2)*v1fyr;
    balls[i].yVelocity = sin(phi)*v1fxr + sin(phi+PI/2)*v1fyr;
    balls[j].xVelocity = cos(phi)*v2fxr + cos(phi+PI/2)*v2fyr;
    balls[j].yVelocity = sin(phi)*v2fxr + sin(phi+PI/2)*v2fyr;
}

Most of these variables need to be floats, and you need to include the <math.h> library to get the functions we need here. The 1 in each variable refers to ball 1, and the 2 to ball 2. The normal and tangential velocities are vn and vt in the above. Don’t worry about the derivation of all of this, this is not a math (or trig) course!

Of course, you need to complete the code with appropriate declarations for any new variables, butwith this addition, you should have your balls bouncing around nicely (but maybe pretty fast. Adjust the speed for now to fix that.)

Bouncing off Walls¶

Poolball Implementation¶

Who Watches For Collisions?¶

Moving a bunch of balls¶

Bouncing off the walls¶

Bouncing off each other¶

Page contents

Previous page

Next page

This Page