Functions That Call Themselves

This idea is a bit shocking to beginners.

Suppose you iare writing the code for a function, and it occurs to you that using the same funciton you are writing to solve the problem you are trying to solve would help. How would that work?

Let’s consider the classic first example of this.

Factorial

You should have learned about this at some point in your math classes:

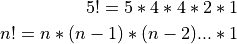
5! = 5 * 4 * 4 * 2 * 1 n! = n * (n-1) * (n-2) ... * 1

But wait!

n! = n * (n-1)!

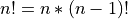
This looks interesting. However, there is a catch to this formula. It does not work for any value of n, and we need a way to stop it.

That way is found by noting that 1! is simply 1. That is called a base case. The factorial of any other (positive) value of n can be figured out using that simple “recursive” formula.

But what does it look like in code?

main.cpp
1
2
3
4
int fact(int n) {
    if (n == 1) return 1;
    return n * fact(n-1);
}

That is about as simple as it gets! We have produced a short chunk of code that should work. It is hard to mess up a piece of code this short. But does it work?

Here is the entire program:

main.cpp
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>

int fact(int n) {
    if (n == 1) return 1;
    return n * fact(n-1);
}


int main(int argc, char ** atgv) {
    int n[] = {1, 2, 3, 7, 9, 20};

    std::cout 
        << "Calculating the factorial of some numbers"
        << std::endl;
    for (int i= 0; i < 6; i++) {
        std::cout 
            << " The factorial of "
            << n[i]
            << " is "
            << fact(n[i]) 
            << std::endl;
    }
}



$ g++ -o demo main.cpp

$ ./demo
Calculating the factorial of some numbers
 The factorial of 1 is 1
 The factorial of 2 is 2
 The factorial of 3 is 6
 The factorial of 7 is 5040
 The factorial of 9 is 362880
 The factorial of 20 is -2102132736

Tilt! There is a problem with that last value. We exceeded the capacity of a simple int and generated a number that would not fit into the container. C++ let us do that, and the result displayed as a negative number. (Why thta happened is something oyu will earn about in your architecture class!)

Let’s try that again, changing the return data type to a long long:

main.cpp
1
2
3
4
long long fact(int n) {
    if (n == 1) return 1;
    return n * fact(n-1);
}

$ g++ -o demo main.cpp

$ ./demo
Calculating the factorial of some numbers
 The factorial of 1 is 1
 The factorial of 2 is 2
 The factorial of 3 is 6
 The factorial of 7 is 5040
 The factorial of 9 is 362880
 The factorial of 20 is 2432902008176640000

Much better. That long long data type sure let’s us calculate some bit numbers! If that is not big enough, clever programmers have found ways to work with huge numbers! All it takes is some “class” programming!

Here is another classic recursive problem:

The formula for a Fibonacci Number for some parameter “n” is defined as:

  • F(0) = 0

  • F(1) = 1

  • F(n) = F(n-1) + F(n-2)

In this case, there are two `base cases, one for 1 and one for 0. Here is the code:

main.cpp
1
2
3
4
5
long long fibo(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fibo(n-1) + fibo(n-2);
}

here is this code in action:

$ g++ -o demo main.cpp

$ ./demo
Calculating the Fibonnaci number for some numbers
 The FIbonacci number for 1 is 1
 The FIbonacci number for 2 is 1
 The FIbonacci number for 3 is 2
 The FIbonacci number for 7 is 13
 The FIbonacci number for 9 is 34
 The FIbonacci number for 20 is 6765

Using Recursion on Linked Lists

If you think about it, a linked list is a recursive thing as well. We start off with an empty list, then add a node. If we are using a simple node object, with a number and a pointer to the next node in the list, that “next node” pointer is NULL, indicating that it is the last one in the list. If we add one more node to the end, we have yet another linked list, this one consisting of a head object, and what can be considered as another linked list (with one item in it). By making use of this fact, we can write routines that access our list using recursion.

As a refresher, here are the original routines we used to build a simple linked list of names:

main.cpp
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include "LinkedList.h"
#include <string>

int main(int argc, char ** atgv) {
    LinkedList myList;
    std::string names[] = {
        "barney",
        "herman",
        "alice",
        "alfonz"
    };

    for (int i = 0; i < 4; i++) {
        myList.insert(names[i]);
    }
    std::cout
        << "List Length = "
        << myList.count()
        << std::endl;
    myList.print();
}
LinkedList.h
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
#pragma once
#include "Node.h"
#include <string>

class LinkedList {
    public:
        Node * head;
        LinkedList();
        void insert(std::string val);
        void print(void);
        int count(void);
};
LinkedList.h
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include "LinkedList.h"
#include "Node.h"
#include <iostream>

LinkedList::LinkedList() {
    head = nullptr;
}

void LinkedList::insert(std::string val ) {
    head = new Node(val, head);
}

void LinkedList::print(void) {
    Node *ptr = head;
    while (ptr != nullptr) {
        std::cout << ptr->name << std::endl;
        ptr = ptr->next;
    }
}

int LinkedList::count(void) {
    int count = 0;
    Node *ptr = head;
    while(ptr != nullptr) {
        count++;
        ptr = ptr->next;
    }
    return count;
}
Node.h
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
#pragma once
#include <string>

class Node {
 public:
    std::string name;
    Node * next;

    Node(); 
    Node(std::string val, Node * nextNode );
};
Node.cpp
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
#include "Node.h"
#include <string>

Node::Node() {
    name="";
    next = nullptr;
}

Node::Node(std::string val, Node * nextNode) {
    name = val;
    next = nextNode;
}

In this example, we add new nodes to the head of the list, but we could modify our LinkedList management class and keep track of the end (tail) of the list easily, and generate routines to add new nodes to the end if that makes more sense to your problem.

The routines we wrote to access the list, specifically, the LinkedList::print and LinkedList.count methods, both use a while loop to walk down the list. The first routine prints out the names in each node, and the second routine simply counts the number of nodes in the list.

$ g++ -o demo main.cpp LinkedList.cpp Node.cpp

$ ./demo
List Length = 4
alfonz
alice
herman
barney

Resursive Replacements

Let’s replace both of these iterative (looping) routines with methods that use recursion to do the same job:

To make these routines recursive, we will need to change the prototypes for both methods, and hand them a Node pointer. Here are the new method prototypes in LinkedList.h:

LinkedList.h
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
#pragma once
#include "Node.h"
#include <string>

class LinkedList {
    public:
        Node * head;
        LinkedList();
        void insert(std::string val);
        void print(Node * ptr);
        void print_reverse(Node *ptr);
        int count(Node * ptr);
};

And here are our modified methods:

LinkedList.cpp:
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void LinkedList::print(Node *ptr) {
    if(ptr == nullptr) 
        return;
    else {
        std::cout << ptr->name << std::endl;
        print(ptr->next);
    }
}

int LinkedList::count(Node *ptr) {
    if(ptr == nullptr) 
        return 0;
    else
        return 1 + count(ptr->next);
}

void LinkedList::print_reverse(Node *ptr) {
    if(ptr == nullptr) return;
    else {
        print_reverse(ptr->next);
        std::cout << ptr->name << std::endl;
    }
}

You need to look closely at these routines. The print method wakes up with a parameter that points to some Node. If that pointer is nullptr, we have hit the end of the list, so we have nothing to print. If the pointer is not nullptr, then we print the current name in that node, and recursively call the same method passing in the address of the next node in the list. It should be obvious that this will generate the same list of names we saw in our original code that used a while-loop.

The count routine works in a similar way. If the pointer we wake up with is nullptr, we return a zero. If it is not nullptr, we return 1 plus whatever is returned from the recursive call to the same routine which we hand the address of the next pointer to as a parameter. Once again, this gives the same answer as the original code.

$ g++ -o demo main.cpp LinkedList.cpp Node.cpp

$ ./demo
List Length = 4
alfonz
alice
herman
barney

Just for fun, here is a recursive routine that prints out the list of names in reverse order. See if you can see how it works:

LinkedList.cpp
1
2
3
4
5
6
7
void LinkedList::print_reverse(Node *ptr) {
    if(ptr == nullptr) return;
    else {
        print_reverse(ptr->next);
        std::cout << ptr->name << std::endl;
    }
}

The slight variation in this print routine is enough to print our the list of names in reverse order! Cute!

Here is the new main.cpp we need to demonstrate these new methods:

main.cpp
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include "LinkedList.h"
#include <string>

int main(int argc, char ** atgv) {
    LinkedList myList;
    std::string names[] = {
        "barney",
        "herman",
        "alice",
        "alfonz"
    };

    for (int i = 0; i < 4; i++) {
        myList.insert(names[i]);
    }
    std::cout
        << "List Length = "
        << myList.count(myList.head)
        << std::endl;
    
    std::cout << "\noriginal list:" << std::endl;
    myList.print(myList.head);

    std::cout << "\nList in reverse order:" << std::endl;
    myList.print_reverse(myList.head);
}

Here is what we get when we run this new version:

$ g++ -o demo main.cpp LinkedList.cpp Node.cpp

$ ./demo
List Length = 4

original list:
alfonz
alice
herman
barney

List in reverse order:
barney
herman
alice
alfonz

Comparing the methods

In general, once you get the hang of writing recursive routines to access these dynamic data structures, I think you can see that the code is a bit easier to write (and is certainly shorter). However, there is a price to pay for this simplicity. Every time you call a method, space is allocated for that method on the system “stack” (yet another data structure that lets us use procedures). That space is occupied until the method returns, then it is released for other methods to use. If your method recurses (!) too deeply, you can run out of memory. This is not a problem, if your write the routine using loops instead.

So Which is better?

For every recursive routine you write, there is an equivalent non-recursive method that will do the same thing. In general, the non-recursive routine will be harder to write, and may be easier to write wrongly. So, most of the time, it is probably better to start off writing recursive routines if you can, then rewrite them if you need more speed, and need to use less memory to get your job done.

As you study more complex data structures, you will find many opportunities to write simple recursive routines to access the data you store in these structures. This introduction should help you get started in that part of your learning! Data structures are extremely important in writing real, complex, programs!