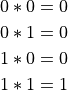Boolean Algebra¶
Read time: 21 minutes (5299 words)
Math can be a lot of fun. (OK, many folks cannot believe math can ever be called fun, but over the course of history, it sure has gotten a lot of attention.)
Here is George Boole:

Way back in 1854 George Boole published a book [Boo54] where he studied the mathematics of a number system with only two symbols: “0” and “1”. We can also call those two values true or false if we wish, but let’s stick with our familiar numbers.
Note
By the way, one of George’s famous papers is part of “God Invented the Integers”, a collection of famous math works edited by Stephen Hawking. [Haw07]. This book is tough to read, but worth the effort!
George wanted to understand how a system of mathemetics would work if restricted to just those two values. His theories have became known as Boolean algebra and are important to us computer folks. His work was recognized as a foundation for computer systems that also work with just two states: on and off. (For some reason, computer folks still insist on saying machines work with “ones” and “zeros”, but it really is not so.)
Arithmetic¶
The basic arithmetic operations we are all familiar with are the first place we run into something interesting. A few results work just fine. Let’s start off by considering addition:
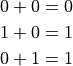
But what about this next one?
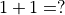
Instinctively, you want to write down “2”, but there is no such number in this system. In binary the result should be “10”, which is also illegal in this system. The only result that makes sense (at least to George) is “1”, since it surely cannot be “0” (the only other possibility)!
So:
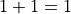
In fact, using this philosophy, the following is also true:
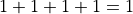
Now that seems just plain silly, and hardly useful. But it really leads to something very useful!
Subtraction¶
Subtraction does not really make much sense, since, by definition, subtraction is identical to addition of negative numbers, which do not exist in George’s boolean world. So we will ignore that operation.
Division¶
Once again, we run into another problem, just as with subtraction. Division is repeated subtraction, and we eliminated that operation. So, division goes out as well!
That is all we need for now. But exactly why this form of math is useful needs to be explored.
Truth Tables¶
Remember back when you were learning about “logical expressions”? You should have been introduced to truth tables, which showed exactly how the logical operators worked. Here is a refresher:
Op |
in1 |
in2 |
out |
|---|---|---|---|
AND |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
OR |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Do you see a pattern here? The truth table for the AND operator follows George’s math rules for multiplication, and the table for the OR operator follows George’s math rules for the addition opeator! Interesting!
Boolean Variables¶
Let’s add variable names to our system. Convention says these are single capital letter names. (I capitalize things to yell at myself. This is to remind me that the variables only have two possible values!)
Assume a variable A has some boolean value. The compliment (opposite) of
that value is denoted using a bar over the variable name. Like this:
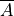
The rules for this notation look like this:
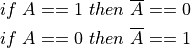
Boolean Algebra¶
With these definitions in place, we can define a few rules for boolean algebra. Most of these should be obviously true.
Note
In the formulas presented below, we will follow standard conventions and use the standard math operator “+” to denote OR and the standard math operator “*” to denote AND. (Personally, I really wanted addition to use that AND operator, because it seemd to make sense. But not to George. I finally got over that urge!)
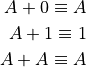
(Boy, that last one probably makes your head hurt! Remember, this is Boolean Math)
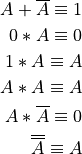
That last one works for any even number of compliments!
There are a few other rules that are useful.
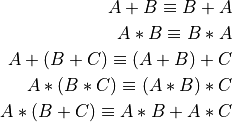
These formulas are useful because there is an equivalence between boolean algebraic formulas and digital circuits involving the fundamental components (aka gates) we use to build them. We can actually set up digital circuits as boolean expressions, then simplify those expressions and produce a simpler circuit that operates the same way. This is a key concept in designing digital systems.
As an example of simplifying a boolean expression, let’s prove the following:
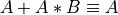
See if you can follow this sequence of operations:
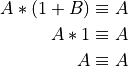
This sequence can be produced by applying the rules shown above using familiar algebraic operations. * De Morgan’s Theorems ***************
There are a few more rules that are very useful in simplifying boolean expressions (circuits) They were developed by Augustus De Morgan, and named after him.
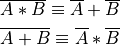
Again, these are very handy when we need to simplify an expression. Simpler expressions lead to fewer components and lower cost. They might also lead to more speed, and we like that!
Exclusive OR¶
There is one more logical operator that is very useful in digital design: The XOR operator. This operator has the following truth table:
Op |
in1 |
in2 |
out |
|---|---|---|---|
XOR |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
The operator produce a “1” if and only if one of the two inputs is a “1”. It produces a zero otherwise.
This operator often appears in Boolean Algebra as a funny symbol in some texts, but we can do better. Since we have eliminated subtraction from our system, let’s use the minus sign as the operator. This has unexpected consequences, but Boolean Algebra seems to have lots of those:
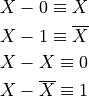
We will develop a couple of additional rules involving this operator later.