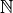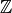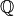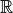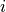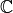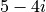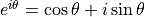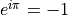Human Numbers vs Digital Numbers¶

Read time: 24 minutes (6196 words)

Now that you know how we store digital numbers in memory, what does this mean when we compare “normal” math to the math computers do?

The answer is subtle, but very important.

In one of your math courses, surely you were introduced to the concept of a number line. That is a line stretching out to infinity in the positive direction, and to negative infinity in the negative direction. “Numbers”, as we were trained to think of them back then, are just points along that line somewhere.

Simple.

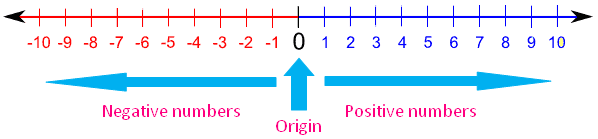
Mathematicians love this picture. They can talk for hours about how operations like addition, subtraction, and multiplication work. When they get to division, things get messy!

Human Kinds of Numbers¶

In your math class you may have been introduced to several different kinds of “Human” numbers.

Natural Numbers¶

Symbol: $\mathbb{N}$

Natural numbers are whole numbers, we use for “counting”. We may include zero in this set of numbers. Another term for these numbers is unsigned. There are no “fractional” numbers in this set. These numbers fall at specific, evenly spaced points on that “number line”, headed off toward infinity

Integers¶

Symbol: $\mathbb{Z}$

Integer numbers are also a form of counting, but what does it mean to have -5 sheep? I guess you rented some, and have to subtract that number from the number you own! Again, these have no fractional part.

Rational Numbers¶

Symbol: $\mathbb{Q}$

Rational numbers represent numbers that can be expressed as the ratio of two integers. That means a whole number divided by a whole number. A number like 1/3 is rational, even if we cannot write it down as a number with a decimal point. (You need too many digits needed to express it exactly!)

Real Numbers¶

Symbol: $\mathbb{R}$

Real numbers are expressed using a decimal point. These numbers can have an infinite number of digits on either side of the decimal point, and can be either positive or negative. Potentially, every point on that number line can be expressed as a Real Number.

Every rational number is also a real number.

Irrational Numbers¶

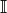
Symbol: $\mathbb{I}$

Irrational numbers are numbers that are not Rational. Simple enough! That means every other number except for those that are rational on that number line .

Every irrational number is also a real number.

Imaginary Numbers¶

Symbol: $i$

Boy, if ever a number ought to be called irrational, it is the number representing the square root of -1! We all know that no such number exists. However, in the world of mathematics, it turns out very handy to pretend that such a number exists, and we call it an imaginary number.

Complex Numbers¶

$\mathbb{C}$

If we combine two numbers, one real, and one imaginary, and plot them on a graph, with the real numbers representing points along one axis, and imaginary numbers representing points along the other axis, we map out something called the complex plain. We write a complex number as the sum of a real part, and an imaginary part.

$5-4i$

By the way, the number zero is both real and imaginary.

Euler’s Formulas¶

Using complex numbers we are able to understand a lot about how electricity works. This kind of math is a big part of the study of electronic devices that make up our digital world.

I am reading a book on Euler’s Formula [Sti17]:

$e^{i\theta } = \cos{\theta} + i\sin{\theta}$

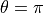When $\theta = \pi$ this becomes this amazing formula:

$e^{i\pi} = -1$

How on Earth did he come up with that? The book lays it out.

Euler's formula is "the most remarkable formula in mathematics"

Richard Feynman

Computer Numbers¶

Computer numbers are very different. For one thing, there is no way we can have an infinite number of them! We only have so many bits to encode them and land them in our memory. Infinity? That is not going to happen in a computer!

The easiest way to visualize digital numbers is simple to place specific marks on the number line. This works for both Integer numbers and Floating point numbers. Those spots mark places where our digital numbers coincide with human numbers. Any other human number simply cannot be represented in a machine, unless we come up with a different encoding scheme.

Furthermore there are boundary points beyond which any given number container (with some fixed number of bits) can’t handle bigger values. Beyond those barriers, we cannot store the values. If we need to process bigger numbers, we need to increase the size of our containers!

Computer Math¶

Think about arithmetic operations using integers. All operations except division are well behaved. They always create integer results, and we can represent those answers exactly with our machines, as long as we have enough bits available.

When we deal with division, things get messy. If we want to express the result of the division as an integer number, we basically take the nearest whole number smaller (back toward zero) than the “correct” human result. (One divided by two is one half, we just “know” that is right. But in the computer world, there is no integer number with that value. We drop the fractional part leaving the integer result: zero!

Warning

You might not believe how hard it is to get humans to understand that simple concept!

Errors Accumulate¶

Humans write programs. They really want the results of their math operations to generate the “correct” answers. But machines can never be expected to be able to express every “correct result. They may easily be off.

If the machine was off on one calculation, then uses that number in further calculations, the errors can increase. (In some rare cases, the may actually improve, but we will ignore that).

The best we can do is find the best “digital number” closest to that human “correct” number and accept that result. We may be “off” by some hopefully small amount, but we are off in many cases! Furthermore, we can study how we do our math and learn how to minimize these errors. That is precisely what I did as a “Computational Fluid Dynamicist” years ago!

Note

There are classic examples of this kind of cumulative math errors resulting in totally wrong answers. If done wrong, your math can be very bad, done right, and things work as expected. I saw an example of this in college where we were “inverting” a matrix of whole numbers, and the “correct answer also was another matrix with whole numbers. However, our simple computer programs trying to get that “correct” answer produced gibberish. Scary, but we got the point.

There is an entire branch of mathematics that explores these issues. You will run into it at some point in your career: Discrete Math!