Decoding Dilema¶
Read time: 33 minutes (8341 words)
Chip designers live in a world of compromises. They have a bunch of parts they need to wire together, and a bunch of wires they need to route from point to point They must find a way to accomplish that, and factor in spacing problems, heat problems, electrical noise problems.
Sheesh! It is a miracle that they even get this work done. In the modern world, most of those issues are addressed by software developed to find optimal solutions to a problem with way too many variables. When the smoke clears, we have a way to encode every instruction we want, and have packed all of the choices into a compact chunk of bits called an instruction opcode.
Our job as decoders is to unravel this seemingly chaotic mess and figure out which instruction we are looking at when we fetch a chunk of that instruction.
The Decoding Mess¶
The chip manufacturer provides a detailed list of all available instructions for the chip. I put all of that data into a single JSON data file so I could study the bit patterns they came up with. It was pretty obvious that there were groups of instructions that you could identify by looking at the first four bits of the instruction. Unfortunately, the remaining 12 bits are still a mess, but you soon discover that there are only a few different ways they smashed together needed data into these bits.
But how can we find usable patterns in the encoding that we can use to decode things?
Enter Python¶
Python has tons of useful libraries, either packaged with the language, or easily downloaded into your system as you find a use for them. JSON processing os a simple task for standard Python (one of the reasons I built that JSON data file in the first place!)
All we need to do it get Python to read the JSON data file, and sort things so we can look for patterns.
Just a quick review of the encoding data shows us that examining all of the encodings in nibble format will be helpful. When I entered the encoding data for each instruction, I created a string with 4-bit groups of codes separated by spaces. This makes it simple for Python to break up the encodings. Then I constructed a complex dictionary, keyed by each 4-bit pattern. Python can sort the keys in a dictionary easily, so in the end, what I came up with was a list of 4-bit codes, four levels deep, each sorted and able to show which instructions share a particular bit pattern.
Without getting too deep into the process, here is the python code I came up with:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | import json
import sys
JDATA = "ATtiny85.json"
class Decoder:
def __init__(self, filename):
try:
fin = open(filename)
except:
print("Cannot open data file")
sys.exit(1)
self.jdata = json.load(fin)
def dump(self):
patterns = {}
for j in self.jdata:
# patterns are nested dictionaries keyed by nibble patterns
bits = j["Bits"]
nibs = bits.split()
n1 = nibs[0]
n2 = nibs[1]
n3 = nibs[2]
n4 = nibs[3]
instruction = j["Mnemonic"]
try:
instruction += " " + j["Operands"]
except:
pass
if not n1 in patterns:
patterns[n1] = {}
if not n2 in patterns[n1]:
patterns[n1][n2] = {}
if not n3 in patterns[n1][n2]:
patterns[n1][n2][n3] = {}
if not n4 in patterns[n1][n2][n3]:
patterns[n1][n2][n3][n4] = {}
patterns[n1][n2][n3][n4]["inst"] = instruction
patterns[n1][n2][n3][n4]["bits"] = bits
n1keys = sorted(patterns)
print("\n\n")
for m1 in n1keys:
print(m1)
level1 = patterns[m1]
n2keys = sorted(level1)
for m2 in n2keys:
print ("\t",m2)
level2 = level1[m2]
n3keys = sorted(level2)
for m3 in n3keys:
print("\t\t",m3)
level3 = level2[m3]
n4keys = sorted(level3)
for m4 in n4keys:
print("\t\t\t", m4, level3[m4])
if __name__ == "__main__":
print("Sorting");
jloader = Decoder(JDATA)
jloader.dump()
|
Running this produces a listing showing all of the patterns and how each instruction defined for our little chip are sorted out.
Note
I placed a copy of the JSON data file, and the reference document used to
generate the data in the files folder now in the CPUfactory3
repository.
I am not going to show the entire output listing here, but we will look at a piece of that output:
1111
00kk
kkkk
k000 BRLO k
k001 BREQ k
k010 BRMI k
k011 BRVS k
k100 BRLT k
k101 BRHS k
k110 BRTS k
k111 BRIE k
ksss BRBS s, k
01kk
kkkk
k000 BRSH k
k001 BRNE k
k010 BRPL k
k011 BRVC k
k100 BRGE k
k101 BRHC k
k110 BRTC k
k111 BRID k
ksss BRBC s, k
All of these instructions share a common pattern. The bits labeled “k” need to
be collected into a single constant. There are 6 bits total in the encoding,
and the legal values are 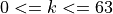 . If you look closely, you
discover that the three low bits in the third nibble are counting their way
through a set of individual instructions.
. If you look closely, you
discover that the three low bits in the third nibble are counting their way
through a set of individual instructions.
Note
The last instruction in each group is just another way of writing the same instructions shown above. We really do not need those instructions, so we will ignore them in our decoder.
We can use nested C++ switch statements to decode this. All we need to do is unpack some bits into useful integers, then set up our switch statement:
Let’s try this out and see what we can build.
Bit Twiddling¶
The C language was invented at a time when lots of programmers worked in
assembly language. There were all kinds of instructions that could examine
individual bits in a packed pile of bits. When C came along, they made sure
that bit twiddling was still possible. The logical operators can be used to
help out:
&logical AND on a set of bits
|logical OR on a set of bits
^logical XOR on a set of bits.
Each of these operators uses a pattern of zeros and ones to do the magic.
The & operator can be used to “mask off” certain bits. Just create a mask
with ones where you want to keep the bits, and zeros where you want to remove
bits, then use the expression num & mask to strip off the unneeded bits,
making them all zero.
The | operator can be used to set certain bits, but we will not be using
that here.
The ^ operator can be used to “toggle” bits, again something we do not
need at the moment.
Finally, we can use the shift operators (>> and <<) to slide bits left
or right. Any bits that “fall off” of either end are just deleted. As we slide
bits, zeros are added to the appropriate end. This is quite handy when you have
the right bits in a group in a packed set of bits, and just want to slide them
into position so they become a normal integer number.
We will use these operators to unpack the needed data items to identify a particular instruction.
Ready, Let’s give this a try!
Here is a random instruction (well, it will be one of those shown in that list above:
uint16_t inst = 0b1111010101010010;
Unpacking the instruction¶
All of our example instructions are 16-bit encodings, but we need the four nibbles to work with. We can use the masking and shifting tricks to isolate those nibbles:
1 2 3 4 5 6 7 8 9 10 11 | // isolate the four nibbles
int n1, n2, n3, n4;
n4 = inst & 0x000f;
n3 = (inst >> 4) & 0x000f;
n2 = (inst >> 8) & 0x000f;
n1 = (inst >> 12);
std::cout << "\t"
<< std::bitset<4>(n1) << " "
<< std::bitset<4>(n2) << " "
<< std::bitset<4>(n3) << " "
<< std::bitset<4>(n4) << std::endl;
|
I am using the bitset class simply to display the data item in binary, to
make sure I get the nibbles split out correctly.
The heart of the action involves masking and shifting to get the bits needed in
the right spot. The common mask is just 0x000f, this has our bits at the
far right of a 16-bit number. I then use the right-shift operator to slide each
nibble into position, where I use the mask to make sure that ony the right-most
four bits remain in each nibble. The data item produced is still 16-bits big,
but the left-most 12-bits are definitely all zeros after this operation!
Note
You should be working to visualize what is happening in these operations. We are not thinking of this pile of bits as a number any more. They are just a set of bits sitting in a list, and we are manipulating them to get the bit pattern we want.
Let’s see this in action:
Unpacking: 62802 (1111010101010010)
1111 0101 0101 0010
That was pretty simple. Not quite as easy as doing things like this in Python, but C++ can do it once you learn the tricks!
Now, we can set up our first level switch statement:
1 2 3 4 5 6 7 8 | switch (n1) {
case 0b0001:
break;
case 0b1111:
break;
default:
std::cout << "invalid code" << std::endl;
}
|
I left out most of the case lines, but for the general decoder, we do need
them. We are using the first nibble from the instruction to break up our logic
into more manageable segments. If you run the Python program on the JSON data
file, you discover that many instruction groups will be pretty easy to decode.
Others, not so easy (UGH!)
We will not run this example, since we are just getting started.
From the Python output above, we see that there are two bits in n2 that
select the group of instructions we need. Extracting that is another example of
sliding the bits into place:
1 2 | // isolate the group selector
int sel = (n2 >> 2);
|
We also need to break out the three bits that select the right instruction from the group we just identified. Here is the (slightly complex) code needed to get the “k” value, and that second selector number:
1 2 3 | // extract "k" and inst selector
int sel2 = (n4 & 0b0111);
int k = ((n2 & 0b0011) << 5) + (n3 << 1) + (n4 >> 3);
|
Make sure you see how shifting and masking managed to put together the “k” value.
Note
42 is such a nice number, look at the bit pattern needed to set that number up!
We have everything in place to decode our instruction now. Here is the nested switch statement that will do the job:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | // decode this instruction
switch (n1) {
case 0b1111:
switch (sel) {
case 0b00:
std::cout << "\tgroup 0" << std::endl;
switch (sel2) {
case 0b000:
break;
case 0b001:
break;
case 0b010:
break;
case 0b011:
break;
case 0b100:
break;
case 0b101:
break;
case 0b110:
break;
case 0b111:
break;
}
break;
case 0b01:
std::cout << "\tgroup 1" << std::endl;
switch (sel2) {
case 0b000:
break;
case 0b001:
break;
case 0b010:
std::cout << "\t\tBRPL " << k << std::endl;
break;
case 0b011:
break;
case 0b100:
break;
case 0b101:
break;
case 0b110:
break;
case 0b111:
break;
}
break;
}
break;
default:
std::cout << "invalid code" << std::endl;
}
|
Although that is tedious to set up it should make sense. Here is the output:
Unpacking: 62802 (1111010101010010)
1111 0101 0101 0010
group 1
BRPL 42
At each level in decoding this instruction, we identify a selector pattern that several instructions share. Each time we discover that several instructions share a particular encoding, we use another nested switch statement to identify the particular selector pattern we need, and home in on the exact instruction.
Our decoder unit will probably be the biggest part of the simulator, which is
why I am limiting the instructions we need to worry about. In my experiments, I
am working on the full instruction set. It is not exactly hard work, but it
takes time to set up. Those selectors we decoded in this experiment show how to
get at the bits you need to define the operation of the machine. For these
instructions, all we really need is that constant k value. We will send
that on to the execute stage for processing, perhaps with additional data from
the sel2 value to identify exactly what these instructions need to do. More
on that later.
Hmmm, maybe I need to train my Python tool to write the C++ code. Such tricks have been used before!
