Lab 10 - Building a module¶
In the lecture this week we explored building a module named mymath.py. In
this lab we will add another function to the module and learn a bit about how
the computer figures out those funny trigonometric functions along the way.
(Have not taken trig yet? Don’t worry, you will before you get out of this
school!)
Computing the sine of an angle¶
Long ago, mathematicians wanted to calculate the trig functions that were
needed to figure out how long the edges of triangle would be. Triangles were
very useful, but they could come in many different shapes. For a
right-triangle, one with two of the three edges coming into one corner 90
degrees from each other, they came up with a few formulas like this:
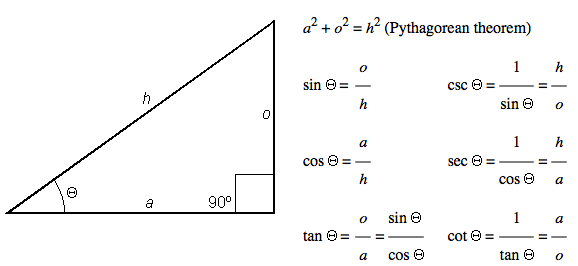
Now, in this class, we do not really care about all those funny functions like
sin, cos, or even tan, but the relationships fascinated the math
folks. Enough so that they started wondering how to calculate something like
sin(x) (where x is the angle between the base and the edge leading up
to the far corner). What they came up with is interesting as well. They
discovered that if you computer the terms in a series of simple expressions
and summed them up, you would get the value you were interested in. For the
sin function, what they came up with was this:
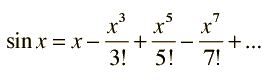
The only problem with all this is that the angle between those two edges needs
to be expressed in terms of something called radians. The formula for
radians is this:
radians = degrees * PI / 180.0
That solves that problem!
Look closely at this series. There is a pattern in what we see. Let’s see
if we can see the pattern:
The series is a sequence of simple terms combined together
After the initial
xterm, each part hasxraised to an odd power starting with 3, and the power goes up by 2 each term.The denominator is the
factorialof the power!The sign of the term alternates between plus and minus
The magnitude of each term gets smaller and smaller as we go, eventually heading toward zero. When it gets there, we will not really know
Could we come up with some code that generates this sequence, and use that code
to build our own sin function? Of course we can!
Building the sin function for our mymath module¶
What you need to do is set up a loop that will compute each term (after the first one) adding in the new term. The problem we face is figuring out when to stop the calculations. For our experiments we will stop when the new term has a value less than 0.00000001. In order figure this out, we will need to generate four variables in our loop:
power
denominator
sign
term
The first one is easy, we just start off with a value of 2 and add two to the
power each time we run through the loop. For the sign, we can use a statement
like sign = - sign and start off with sign set to -1 to start. That will
make the value flip between plus one and minus one. Finally the term is the
angle (x - in radians) raised to the power and divided by the factorial
part. We multiply that term by the sign and add it in to the result we are
after. See how it works?
That leaves the factorial. Shoot, that looks like another function.
Factorial function¶
The factorial of 5 is 5 * 4 * 3 * 2 * 1 or 1 * 2 * 3 * 4 * 5
A simple function to calculate the factorial looks like this:
def factorial(n):
fact = n
for val in range(1,n):
fact = fact * val
return fact
Does that look right?
Testing your code¶
Since we are building a module, you are to build a test program that uses your
module and the real math module to see how well your code is doing. You
should test the sin function over the range of angles from 0 to 360, in one
degree increments. Look at the example code in the mymath module in the
lecture to see how to get the real sin function in the math module to
give you the real value and see if you are close. (You should be).
Your test program will need to import both your new module and the real
math module:
import math
import mymath
We will discuss how Python finds these files in class.
