Exploring Mandelbrot Space¶
The area inside of which all mandelbrot images can be seen is a square bounded by real and imaginary values ranging from -2 to +2 in each direction. In building a tool that will let the user explore this space, we need a way to set a point of interest, then set the distance from that point in both directions we wish to see. This is a problem in coordinate transformation, that is not hard to figure out, if you are willing to do a bit of that ugly math stuff!
Windows¶
Our first concern is the size of the “window” we have available to see
anything. This window sits on your screen and has dimensions. We hardly ever
worry about the physical dimentsions, like inches and feet, instead, we measure
sceen sizes in “pixels. One pixel is probably pretty tiny, but it is the
location of a single tri-color light emitting diode (usually) that we can color under
control of our computer. It may seem odd to you if you never looked really
closly at your screen, but everything you can see on that screen is composed of
tons of tiny dots, each colored one particular color.
Looking Out¶
When drawing images on the screen, it helps to visualize yourself sitting at a point some distance away from the screen. Pretend that screen is actually a window, and you are looking through that window to some scene beyond the screen. If you draw a line (in 3-D, of course) from any visible point in that outer world, through the screen to your eye, the point where the line intersects the screen needs to be colored exactly what the point at the far end of the line is colored. Now, not every point in the outer world will intersect our screen smack in the middle of one pixel, so maybe it helps to go the other way.
Draw a line from your eye to each pixel on the screen. Then project that line into the world beyond. Where that line hits something, we need to figure out the color that is there, and color our pixel the same color.
By doing this we create an “image” of that world beyond on pur screen, and we can capture that image in a file for later use. This is exactly what a digital camera does!
Geometry Lesson¶
Most of you have taken a geometry class at some time. In that class, you probably learned about ‘similar triangles”. Here is one:
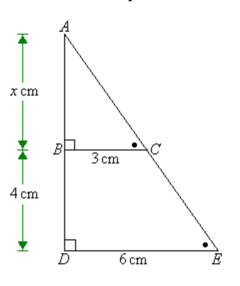
The triangles we are working with ere are ABC and ADE. Both are similar in that the angles on all three corners are identical. That means the lengths of the sides are proportional as well. If the length of AD is twice that of AB, then the side DE is twice that of BC as well. We can use this to calculate where in our Mandelbrot World we need to figure out a pixel color.
Here is how we do that. Let’s put Mandelbrot’s World along the line DE. (Well half of it, we will assume the other half is the same basic size. We will put our screen dimension along BC. Now the units differ, but it is the proportions that matter here.
Suppose half of our our screen is 300 pixels wide (from B to E), that means one pixel happens every 1/300 of that distance. Looking at our Mandelbrot world, if we are plotting from -2 to +2, that means half of that is 0 to 2. One three hundredths of that is the point where a line goes through the screen.
Using these calculations, for ever point on our screen, we can figureout where that point is in Mandelbrpt’s world, and figure out the complex number for that point.
Centering on a Point¶
Most fun images are not centered in the middle of this space, they move over to an interesting point, and zoom in or out. Effectively, we “slide” Mandelbrot’s World sideways some amount, them adjust the Mandlebrot world so it sits closer of further away from the screen. The other way to view this is we simple stretch Mandelbrot’s world, expanding it to see a smaller area in our screen. If we can figure out the new Mandelbrot spacing that cooresonds to our pixel spacing, again, we cna calculate the cooresponding complex number we are looking at.
All of this world sliding and scaling (stretching) amounts to transformations needed to figure out the right complex number for each spot we wish to color on our screen!
See, math can be fun, as long as it results in cool pictures.
We need some controls to help us move around and do the zoom trick.
Pointing to an Interesting Point¶
Specifying a point to center our image on is easy, point to that spot and click the mouse, of course. ard Handler ——————–
Freeglut Mouse Routine¶
Just as we did for the keyboard, we can create a simple mouse handler, and use it to figur eout where on the screen the mouse was when you clicked a button. Here is the code needed for that:
int mousex, mousey;
void showMouse(int x, int y) {
int time = frames;
std::string msg = "Mouse: ";
snprintf(&msg[8], sizeof(&msg[8]), "%4d %4d", x, y);
showString(60, 350, msg);
}
void mouse(int button, int state, int x, int y) {
y = WINDOW_HEIGHT - y;
mousex = x;
mousey = y;
if (button == GLUT_LEFT_BUTTON) {
if (state == GLUT_UP) {
// check all buttons to see if any need attention
if (stop_button.toggle(x, y)) exit(0);
arrow_button1.toggle(x, y);
arrow_button2.toggle(x, y);
delta_count = -delta_count;
}
}
}
Note
This routine is an example, pulled from another project.
Freeglut Keyboard handler¶
We already have a keyboard handler that waits for the user to hit a key on the jeyboard. At present, that handler checks to see if the “q” key was pressed. If so, the program terminates.
All we need to do is add new keys to that code to “zoom in” and “”zoom out”. Figuring out how far to do each is something I iwll leave for your study.
Once we know where we want to look, and how much to zoom our view of the world, the only thng we need to worry about os coloring. EACH spot! And that can be a ton of spots. Good thing we have fast computers.
Coloring¶
Most Mandelbrot images are generated by recursively runnig the complex number chosen through that simple formula:
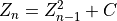
In most systems, the constant C is chosen as the complex number at the point where the calculations start.
All you do to pick a color is to set up a loop that will evaluate Mandelbrot’s
formula over and over. Each time you get a new complex number, you calculate
the magnitude of that number and check the value. If the magnitude exceeded
2.0, you break out of the loop. You need a loop counter to track how many
passes it takes for some number to reach that 2.0 magnitude. You also need a
number that will be used to stop the loop, in case the number never reaches
2.0.
Note
According to Mandelbrot, if the magnitude ever exceeds 2.0, it never comes back. Good to know!
When we stop our loop, either by running it to the ending number, or it finally reached that 2.0 magnitude. We will pick a color. If we reached the loop end value, the color is black. For any other case, we have a number that we need to use to pick a color.
Basically, each point will end up as some integer number, but we do not really know how big the number might be. WHat we need to do it take that number and pick one of several possible values. We can create an array of numbers, each representing a specific color, and use the mod` operator to attack our loop counter number:
color num = loop_counter % num_colors;
We will reuse colors in this scheme, but we will get a way to pich one color for each spot, no mater how big that loop counter managed to get.
Note
This is just one scheme folks have used to pick a color. Others have comeup with more creative ways to pick colors, and the results can be pretty cool!
The last part of the puzzle is to sweep over the entire screen coloring each spot.
for(int row=0; row< SCREEN_HEIGHT; row++)
for (int col=0; col< SCREEN_WIDTH; col++) {
real = col * delta_col;
imag = row * delta_row;
Complex z(real, imag);
color = pick_color(z);
screen[row,col] = color;
}
YOu will need to tune that idea up. More on that next time!.
